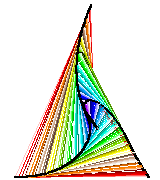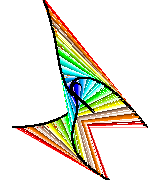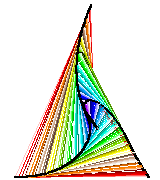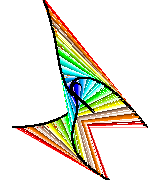MicroWorlds index

Turtlechase Overview

Go to the turtlechase project!

so you can use the project

screenshot of turtlechase (inactive buttons)

3 sample designs drawn with turtlechase (after moving the turtles to new positions)

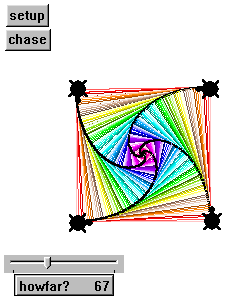
To use this project, you need the free MicroWorlds Web Player, but you do not need to know anything about MicroWorlds. This project explores a question posed to Marilyn vos Savant in Parade Magazine in February 1999: If four [turtles] start out at four corners of a square, and each begins moving towards the next, what path will they follow, and how far will they travel before they all meet in the middle? Marilyn answered that they would follow a partial spiraling path and that the distance each travelled would exactly equal the length of one side of the original square. This project tests her answers and illustrates that she is right! 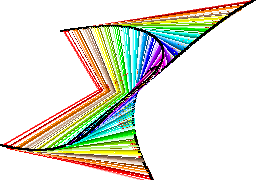(The turtles are instructed to stop after they have each travelled the length of one original side.) There is one invisible turtle racing between the four visible turtles, connecting all four turtles with a square and then switching color, before each visible turtle takes a new step. This helps to illustrate that at all times the four turtles maintain an equal distance - an ever-shrinking square. However, some first-grade students discovered that it is even more interesting to click and drag the turtles around after clicking "setup" but before clicking the "chase" button. You can get some very nice designs. The turtles will not always meet in the middle (and sometimes they will surpass it) after they have been dragged, because they will stop after they have travelled the length of one original side (if they had not been dragged somewhere else). If you own MicroWorlds and would like to create the turtlechase project yourself from scratch, click the arrow to see the procedures.